Последний триместровый экзамен, который мне пришлось сдавать, сильно отличался от всех предыдущих. Мне нравится концепция неординарных экзаменов, но иногда они бывают немного непродуманными и/или забирают слишком много сил у учеников. А так хочется говорить без иронии: «Экзамен для меня всегда праздник!» Но в прошлом триместре, несмотря на то, что нашему классу попались мои самые нелюбимые […]
Тихон Милиневский


лютого 14, 2012 | Тихон Милиневский
Вредят ли литературе графоманы?
Думаю, стоит начать с того, кто такие графоманы. Графоманами называют людей, которые пишут прозу или стихи, но при этом не имеют какого-либо таланта. В словаре ещё объясняют — это психическое заболевание. Презрительное слово. Честно говоря мне кажется, это просто термин, с помощью которого напыщенные «настоящие» поливают грязью начинающих поэтов и постмодернистов-прозаиков, отбивающих у «духовных творцов» хлеб. Этих […]

грудня 21, 2011 | Тихон Милиневский
Прямоугольник с острым углом
В 1776 году известный математик Иоганн Ламберт пытался доказать пятый постулат Евклида. Он рассматривал прямоугольник у которого три угла прямые. Соответственно было три варианта: либо третий угол прямой, либо тупой либо острый. Первый вариант подходит под все утверждения Евклида, и под пятый постулат в частности. Второй вариант расходится уже с первыми четырьмя постулатами — следовательно тупого […]
грудня 20, 2011 | Тихон Милиневский
Мои впечатления о программе Adobe InDesign
Индизайн — достаточно простая, и интуитивно понятная программа. После краткой лекции по её функциям и возможностям я сделал макет, а заполнить его текстом и изображениями уже не составляло никаких проблем. Сложности были в основном в работе с самим текстом. Я выбрал английский стиль оформления колонок, поэтому у меня было много «заборов», а когда я сжимал текст, […]
грудня 19, 2011 | Тихон Милиневский
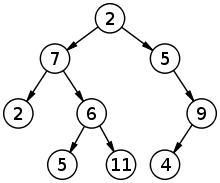
Математический лес
Да, в математике есть деревья, вот только вместо веток у них рёбра, зато хоть листья есть. Математическое дерево выглядит так: Дерево это граф, и это неоспоримо) Кружки называют вершинами, стрелочки, которые их соединяют, это рёбра, а кружки от которых стрелочка не идёт называют листьями. Соответственно точка к которой не идут стрелки это корень. А лес — это […]
 Олексій Греков
Олексій Греков Юлия Корсакова
Юлия Корсакова Татьяна Слободянюк
Татьяна Слободянюк Мария Федорец
Мария Федорец Юлия Ролик
Юлия Ролик Марина Сущенко
Марина Сущенко Марина Осадчая
Марина Осадчая Светлана Питайкина
Светлана Питайкина Наталья Галымова
Наталья Галымова Инна Стах
Инна Стах Виолетта Зиновьева
Виолетта Зиновьева Светлана Продан
Светлана Продан Андрей Руденко
Андрей Руденко Женя Грекова
Женя Грекова Вера Воронина
Вера Воронина Ирина Липкова
Ирина Липкова Татьяна Ефремова
Татьяна Ефремова Оксана Андрейко
Оксана Андрейко Яна Петербуржцева
Яна Петербуржцева Елена Марченко
Елена Марченко Елена Мохорт
Елена Мохорт Ярослава Мозгова
Ярослава Мозгова Валентина Безпала
Валентина Безпала Ганна Котяш
Ганна Котяш Наталия Бова
Наталия Бова Наталья Рубан
Наталья Рубан Галина Подвальная
Галина Подвальная Евгений Чепорнюк
Евгений Чепорнюк Анна Завгородня
Анна Завгородня Виктория Красюк
Виктория Красюк Света Бирюкова
Света Бирюкова Алена Муравьева
Алена Муравьева Ольга Рухлова
Ольга Рухлова Адміністрація Школи
Адміністрація Школи Руслана Самсонюк
Руслана Самсонюк Константин Кудряшов
Константин Кудряшов Вера Орлова
Вера Орлова Вера Талалай
Вера Талалай Тетяна Гах
Тетяна Гах Нина Лапшикова
Нина Лапшикова Алла Слотвинская
Алла Слотвинская Яна Алаверанова
Яна Алаверанова Людмила Шереняк
Людмила Шереняк Маричка Денищук
Маричка Денищук Елена Штеренберг
Елена Штеренберг Олег Князев
Олег Князев Шевхие Чакалова
Шевхие Чакалова Оксана Балакшина
Оксана Балакшина Марина Серебряная
Марина Серебряная Виктор Задояный
Виктор Задояный Дарья Чудопал
Дарья Чудопал Ирина Спиридонова
Ирина Спиридонова Світлана Пітайкіна
Світлана Пітайкіна Владимир Звиняцковский
Владимир Звиняцковский Инна Уляненко
Инна Уляненко Ольга Сорока
Ольга Сорока Инна Ведмидь
Инна Ведмидь Тихон Милиневский
Тихон Милиневский Екатерина Чумак
Екатерина Чумак Ирина Заведея
Ирина Заведея Юрий Денисенко
Юрий Денисенко Ольга Полажинец
Ольга Полажинец Татьяна Швец
Татьяна Швец Лилия Атамась
Лилия Атамась Анна Тарковская
Анна Тарковская Светлана Самойликова
Светлана Самойликова Татьяна Василёва
Татьяна Василёва Дария Котко
Дария Котко Людмила Солодовник
Людмила Солодовник Олеся Бондаренко
Олеся Бондаренко Євген Матинський
Євген Матинський Михаил Левша
Михаил Левша Елена Терёшина
Елена Терёшина Наталья Шевченко
Наталья Шевченко Вика Сенюк
Вика Сенюк Анна Залужная
Анна Залужная Татьяна Шарапова
Татьяна Шарапова Ольга Ломако
Ольга Ломако Сергей Гринкевич
Сергей Гринкевич Павел Новиков
Павел Новиков Юлия Кондрашова
Юлия Кондрашова Ольга Перекопайко
Ольга Перекопайко Ольга Пеховская
Ольга Пеховская Дмитро Приходько
Дмитро Приходько Олеся Выговская
Олеся Выговская Никита Пономаренко
Никита Пономаренко Дар'я Мутиліна
Дар'я Мутиліна Віолета Зінов'єва
Віолета Зінов'єва Нина Червоний
Нина Червоний Елена Масляева
Елена Масляева Аня Пупенко
Аня Пупенко Владислав Сивак
Владислав Сивак Наталья Иванча
Наталья Иванча Даниэлла Калигорская
Даниэлла Калигорская chaikovskaja
chaikovskaja Александра Харькова
Александра Харькова Ирина Паранюк
Ирина Паранюк stetsyna
stetsyna Сергей Биденко
Сергей Биденко Анатолий Новиковский
Анатолий Новиковский Татьяна Ильченко
Татьяна Ильченко Александр Котенко
Александр Котенко Юлия Сенюк
Юлия Сенюк Вика Золотаревич
Вика Золотаревич Алена Мельник
Алена Мельник Людмила Покидько
Людмила Покидько Наталья Смолянюк-Власюк
Наталья Смолянюк-Власюк Петр Дынник
Петр Дынник Елизавета Шинкарева
Елизавета Шинкарева Сергей Касяненко
Сергей Касяненко
